3 Formalization
This section is mostly based on [MBC+06], with some additional stuff from [CDL+06].
3.1 A Summary of Package Metadata
In this section we briefly summarize the features of DEB and RPM packages that are relevant to understand the result of EDOS for dependency management. Where not explicitly stated, these features are to be intended the same in both DEB and RPM package systems. A more detailed analysis of various packaging systems can be found in Section 1.
A package is a binary bundle that contains a component, all the data needed to its correct functioning and some metadata which describe its attributes and its requirements with respect to the environment in which it will be deployed. Packages not always contain “executable” components. Often documentation and non-executable artifacts are packaged as well. However, to our purposes, this distinction is not relevant because the package format is agnostic with respect to its actual content type.
Both DEB and RPM packages are actually compressed archives. However, while RPM is actually an ad-hoc format explicitly conceived for this purpose, DEB packages can be produced using standard tools (i.e., ar and tar), so they can be easily managed. Nevertheless, the most relevant difference between DEB and RPM package format concerns their metadata specification. While RPM packages encode it in a binary form as a part of its ad-hoc archive format, DEB packages use a textual representation for it. This fact makes its processing easier. Figure 9 shows an excerpt of the metadata taken from the firefox DEB package in version 1.5.dfsg+1.5.0.1-2 for the i386 architecture.
Package: firefox Version: 1.5.dfsg+1.5.0.1-2 ... Depends: fontconfig, psmisc, libatk1.0-0 (>= 1.9.0), libc6 (>= 2.3.5-1) ... Suggests: xprint, firefox-gnome-support (= 1.5.dfsg+1.5.0.1-2), latex-xft-fonts Conflicts: mozilla-firefox (<< 1.5.dfsg-1) Replaces: mozilla-firefox Provides: www-browser...
Figure 9: Excerpt of a DEB package metadata
Every package has a version that is used to give a temporal order to the packaged component release. Though the version structure of RPM and DEB packages is the same (i.e., epoch number, version id and revision id), the comparison algorithm is slightly different. Version information is central when specifying relationships between packages.
The kinds of relationships that can be expressed in RPM and DEB package metadata are almost the same, except some very specialized ones that are seldom used or processed (e.g., obsoletes, replaces, suggests, enhances)
In this paper we have taken into account only the three main relationships that are used with the same semantics in both RPM and DEB packages:
- Depends (DEB), Requires (RPM): used to establish a requirement on the packages that must be present in the system in order to make the current packaged component fully functional.
- Conflicts (DEB, RPM): used to establish a requirement on the packages that cannot be present at the same time in the system with the current one. A successful installation can be performed only if no conflicting packages are already present in the system.
- Pre-Depends (DEB), PreReq (RPM): similar to the Depends relationships but used to establish a requirement on the packages that must be already present in the system in order to successfully deploy the packaged component. The difference between Pre-Depends and Depends is that while Depends package might not be present in the system when deploying the packaged component (but only after, so they can be deployed together with the current component), Pre-Depends packages must be already installed even before attempting to deploy the current packaged component.
Relationships are specified by using a list of package names, optionally with version constraints. Each element in the list represents a requirement for the given relationship, and all these requirements must be met (i.e., they are a conjunction) in order to satisfy the dependency relationship. Actually, the DEB package format allows an element of the list to be a disjunction of requirements. This is done by using the | operator. In this case, in order to meet the (disjunctive) requirement it is sufficient that at least one of the constituting requirements is met.
Figure 9 shows that the package firefox version 1.5.dfsg+1.5.0.1-2 has, among the others, a Depends requirement on the package fontconfig and on a package debianutils with a version >= 1.16. This means that once the packaged component firefox is deployed, in order to correctly function, it will need the debianutils component with a version greater than or equal to 1.16 to be deployed as well. When no version constraint is specified, then any packaged component version will do.
The allowed version constraints can be specified by using only the standard comparison operators with their standard semantics: <, <=, =, >= and =.
Depends: libc6 (>= 2.0), xlibs (>= 4.0) | xlib6g (>= 3.3.3.1), ...
Figure 10: DEB disjunctive dependency requirement
Figure 10, on the other hand, shows an example of a disjunctive dependency requirement. In order to correctly function, the current packaged component needs libc6 with a version >= 2.0 and either xlibs with a version >= 4.0 or xlib6g with a version >= 3.3.3.1.
Another essential information is given by the Provides metadata. When specified it allows to declare an identifier that can be used to reference the package. Such an identifier is often called either virtual package or feature. For instance, in Figure 9 the firefox package Provides the identifier web-browser. It is important to point out that this identifier can be used when specifying dependency relationships. So, for example, another package could declare a dependency requirement by specifying web-browser. In this case this requirement should be considered as a disjunctive requirement whose elements are all the packages that provide web-browser.
In RPM metadata, these features are the only way of declaring a relationship between packages; it is not possible to declare a relationship directly between packages, only by way of features. Also, it is worth noting that while RPM does not allow disjunctive dependencies per se, they can be emulated by declaring a dependency on a feature that is provided by two or more packages.
DEB also allows virtual packages, but their usage is strictly limited to a few cases (there is an explicitly maintained list of virtual packages) and using direct relations between packages is the standard practice.
3.2 Formal Model of Package Relations
In this section we formalize the definitions we have described in Section 3.1 and we introduce the notion of package installation that identify the central property we want to guarantee for each package present in a package repository.
Now we have two choices: either we try to represent formally the version constraints used in the different package formats, and then our model will need to take into account relationships between versions like the >=, =, >>, <<, <= found in the Figure 9; or we keep our model simple and eliminate all version constraints but one, equality (==), by replacing all the other version constraints with the explicitly listing of all packages versions that satisfy the version constraints (we call such replacement an expansion). This second choice has the additional advantage that the model becomes independent on the specific version comparison operators, present and future, of any given package format, but of course such expansions are relative to a given repository, so any change to the repository will make it necessary to perform the expansion phase again.
As an example, consider a repository containing versions 0.9, 1.0 and 1.1 of mozilla-firefox. Then the conflict relationship in Figure 9 would expand as shown in Figure 11.
Once this expansion has been performed, we are left only with direct dependency or conflict relationships among actual packages, i.e. (unit, version) pairs, and we can then in a straightforward way encode them it into a graph.
In the following we will hence assume that the distribution is fixed, and that the version comparison operators have been expanded. Notice that, due to this assumption, we can also get rid of all the details concerning the particular ordering over version strings used in common FOSS packages: we use the specific version comparison algorithm only to expand the dependencies, and then we can use any set of unique identifiers for representing each version. One reason why directly working with ordering constraints on version numbers is that the version numbering schemas used in DEB and RPM packages are not discrete: for any two version strings v1 and v2 such that v1 < v2, there exists v3 such that v1 < v3 < v2.
For instance, if the repository of our Debian distribution contains the versions 2.15-6, 2.16.1cvs20051117-1 and 2.16.1cvs20051206-1 of the unit binutils, we may encode these versions respectively as 0,1 and 2, giving the packages (binutils,0), (binutils,1), and (binutils,2).
- The relation C is symmetric, i.e., (π1,π2) ∈ C if and only if (π2,π1) ∈ C for all π1,π2 ∈ P.
- Two packages with the same unit but different versions conflict, that is, if π1 = (u,v1) and π2 = (u,v2) with v1 ≠ v2, then (π1,π2) ∈ C.
The second requirement in the definition of a repository is present in some package management systems, notably Debian’s, but not all. For instance, RPM-based distributions allow simultaneous installation of several versions of the same unit, at least in principle (if, for example, they do not install files in the same location).
In a repository R = (P,D,C), the dependencies of each package p are given by D(p) = { d1, …, dk } which is a set of sets of packages, interpreted as follows. If p is to be installed, then all its k dependency requirements must be satisfied. For di to be satisfied, at least one of the packages of di must be available. In particular, if one of the di is the empty set, it will never be satisfied, and the package p is not installable.
The attentive reader might have noticed that we do not have a separate dependency function for modeling Pre-Depends relationships. In fact, we consider them as if they were normal Depends relationships. This is reasonable because we put ourselves on the distribution editor-side where we have a package repository (and not an installed system). At this level, the two kinds of relationships can be considered equivalent.
|
As described in Section 3.1, dependencies are usually conjunctive, that is they are of the form
| a → b1 ∧ b2 ∧ ⋯ ∧ bs |
where a is the target and b1, b2, … are its requirements. However, more complex dependencies can be specified, with name disjunctive requirements. So the general form for a dependency specification is a conjunction of disjunctions:
| a → (b11 ∨ ⋯ ∨ b1r1) ∧ ⋯ ∧ (bs1 ∨ ⋯ ∨ bsrs). (1) |
For a to be installed, each term of the right-hand side of the implication 1 must be satisfied. In turn, the term bi1 ∨ ⋯ ∨ biri when 1 ≤ i ≤ s is satisfied when at least one of the bij with 1 ≤ j ≤ ri is satisfied. If a is a package in our repository, we therefore have
| D(a) = { { b11, …, b1r1 }, ⋯, { bs1, …, bsrs } }. |
In particular, if one of the terms is empty (if ∅ ∈ D(a)), then a cannot be satisfied. This side-effect is useful for modeling repositories containing packages mentioning another package b that is not in that repository. Such a situation may occur because of an error in the metadata, because the package b has been removed, or b is in another repository, maybe for licensing reasons.
Concerning the relation C, two packages π1 = (u1,v1), π2 = (u2,v2) ∈ P conflict when (π1, π2) ∈ C. Since conflicts are a function of presence and not of installation order, the relation C is symmetric.
- Abundance: Every package has what it needs. Formally, for every π ∈ I, and for every dependency d ∈ D(π) we have I ∩ d ≠ ∅.
- Peace: No two packages conflict. Formally, (I × I) ∩ C = ∅.
Note that because of conflicts, every member of a set X ⊆ P may be installable without the set X being co-installable.
| (Π) = |
| d. |
In simpler words, Δ(Π) contains Π, then all packages that appear as immediate dependencies of Π, then all packages that appear as immediate dependencies of immediate dependencies of Π, and so on. Since the domain of D is a complete lattice, and D is clearly a monotonic function (it is even a continuous function), we immediately get by the Knaster-Tarski theorem that such a smallest set exists and can be actually computed as follows:
| Δ(Π) = |
|
| n(Π). |
The notion of dependency closure is useful to extract the part of a repository that pertains to a package or to a set of packages.
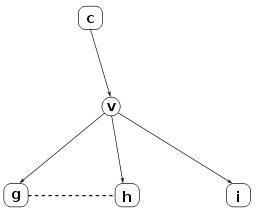
The following graph shows the subrepository generated by the package c of example 1. The dependency closure of c is the set of package nodes of that subrepository, that is {c,g,h,i}.
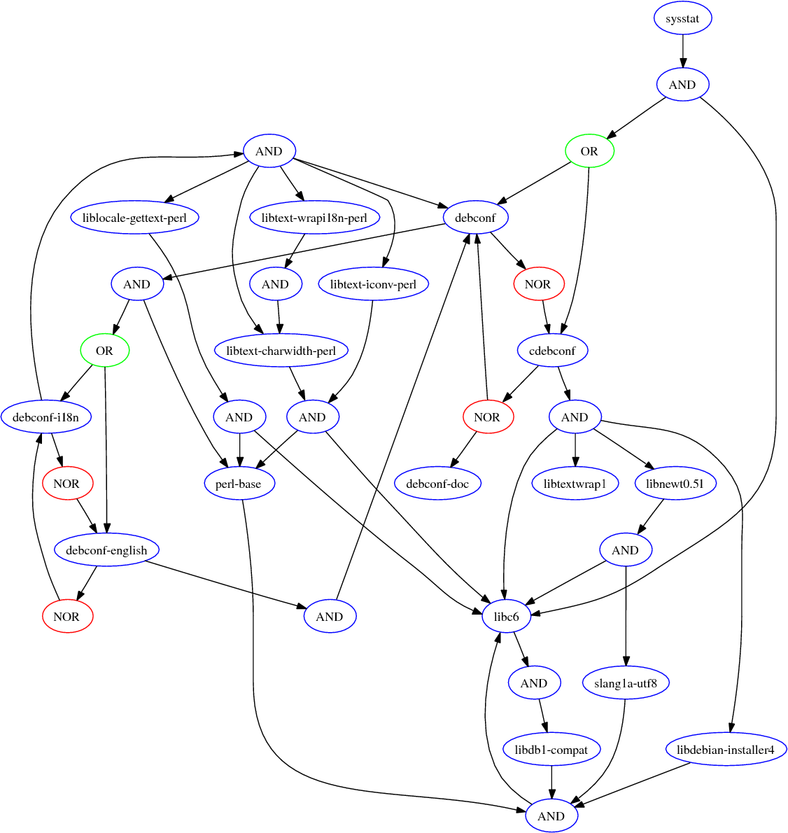
A larger, real-world example is the subrepository generated by the package sysstat in Debian stable on 2005-12-13, viewed as a boolean graph. Version numbers have been omitted for brevity.
We then have the following property, which allows to consider only the relevant subrepositories when answering questions of installability.
The desirable property that we want to ensure over a repository R is the following:
The intuition is that if a repository is not trimmed, then it contains packages that cannot be installed in any configuration: these packages behave as if they were not part of the repository. This means that either they should not be actually there or there is some a problem in their metadata specification that should be corrected.